Kompresja Huffmana

Kody Huffmana to jedna z powszechnie stosowanych metod kompresji danych. Metoda ta jest oparta o strategię zachłanną. Kompresja ta polega na zastępowaniu znaków kompresowanego pliku krótszymi kodami (a ściślej ciągami bitów), dzięki czemu wynikowy ciąg bitów jest znacznie krótszy od wejściowego. Jak wiadomo znaki są kodowane na 8 bitach, dzięki czemu można zakodować aż do 256 znaków (kody ASCII od 0 do 255). Bardzo rzadko się jednak zdarza, by w pliku występowały wszystkie znaki ASCII, wobec tego można wykorzystać mniej bitów i przez to zaoszczędzić dużo miejsca.
Znaki można kodować na dwa sposoby:
Za pomocą kodów o stałej długości
Za pomocą kodów o zmiennej długości
Metoda pierwsza jest bardzo prosta, lecz mniej skuteczna niż druga. Polega ona na przypisaniu znakom liczb porządkowych, np. zał. że nasz plik został zapisany za pomocą znaków alfabetu A={a, b, c, d, e). Alfabet ten składa się z 5 znaków jest to dużo mniej niż 256, nie potrzebujemy więc aż 8 bitów, wystarczą nam 3, gdyż 23=8, za pomocą 3 bitów można zapisać 8 znaków. Gdyby nasz alfabet składał się z 4 znaków, wówczas wystarczyłyby tylko 2 bity, gdyż 22=4.
Załóżmy, że nasz plik ma dokładnie 1MB, czyli 1024*1024=1.048.576 bajtów. Każdy bajt jest kodowany na 8 bitach, czyli nieskompresowany plik zajmuje 8*1.048.576=8.388.608 bitów. Jak zauważyliśmy jednak nam wystarczą po 3 bity na znak. Przypiszmy więc każdemu znakowi liczbę porządkową (zapisaną binarnie): a=000, b=001, c=010, d=011, e=100. Zamiast używać 8 bitowych kodów ASCII używamy własnych 3 bitowych kodów. Sprawdźmy jakie odnieśliśmy na tym korzyści: 1.048.576*3=3.145.728 bitów, czyli 37,5% pliku wejściowego. Całkiem nieźle, zauważmy jednak, że tak dobry wynik osiągamy tylko dlatego, że nasz alfabet miał jedynie 5 znaków. Im większy alfabet, tym gorszy wynik. Przy alfabecie składającym się ze wszystkich 256 znaków będziemy potrzebowali 8 bitów (28=256), czyli tyle ile normalnie.
Alternatywą dla opisanych powyżej kodów o stałej długości są kody o długości zmiennej. Wykazują one lepsze własności dla znaków częściej występujących. Zauważmy bowiem, że lepiej jest przypisać mniej bitów znakom częściej występującym i więcej bitów znakom rzadziej występującym. Wiąże się z tym jednak pewien problem: w przypadku kodów o stałej długości dekompresując plik nie było problemu z pobieraniem kolejnych kodów z ciągu bitów (każdy miał np. 3 bity). Jeśli kody mają różną długość nie wiadomo, kiedy kończy się stary kod a zaczyna nowy. Dlatego należy posługiwać się kodami prefiksowymi tzn. takimi, że żaden kod znaku nie jest prefiksem innego znaku, czyli nie jest częścią początkową innego kodu.
Przykład:
kod 101 jest prefiksem kodu 10111, bo kod 10111 zaczyna się od ciągu 101, będącego pierwszym kodem.
Z kolei kod 101 nie jest prefiksem kodu 100111.
Odczytując kody prefiksowe z ciągu bitów wiemy, kiedy kończy się stary a zaczyna nowy, np. dla kodów prefiksowych 0, 101, 100 nie ma problemu z odczytaniem ciągu 001001010:
Pobieramy pierwszy bit 0: spośród naszych 3 kodów tylko jeden zaczyna się od 0: 0. Odcinamy go i pobieramy następny: znów 0. Po odcięciu dwóch 0 mamy ciąg 1001010, pobieramy kolejny bit: tym razem dwa kody zaczynają się od 1, pobieramy więc kolejny bit: 0 (mamy już 10) i nadal dwa kody do niego pasują, pobieramy więc kolejny bit: 0 i otrzymujemy 100 (trzeci kod), odcinamy go i postępując tak samo dla ciągu 1010 otrzymamy 101 i 0. Tym sposobem rozłożyliśmy ciąg 001001010 na kody 0, 0, 100, 101, i 0, mimo, że mają one zmienną długość.
Istnieje dowód, że za pomocą kodów prefiksowych można otrzymać maksymalny stopień kompresji. Problem przydziału kodów prefiksowych znakom rozwiązał Huffman. Polega on na analizie częstości wystąpień poszczególnych znaków i stosowaniu drzew binarnych postaci:

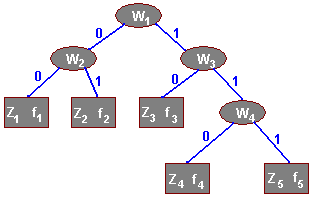
W każdym liściu (prostokąt) znajduje się znak Zi oraz liczba fi oznaczająca częstość wystąpień znaku Z w kompresowanym tekście. W każdym węźle (elipsa) znajduje się liczba W j (waga) będąca sumą liczb W lub f swoich potomków, czyli:
W4=f4+ f5, W2=f1+ f2, W3=f3+ W4 oraz W1=W2+ W3.
Ciekawą cechą kodów Huffmana jest fakt, że reprezentujące je drzewo binarne jest regularne, tzn. każdy węzeł ma dwóch synów.
Na rysunku widać etykiety nadane krawędziom drzewa: 0 dla lewej krawędzi i 1 dla krawędzi prawej. Te etykiety służą do wyznaczania kodu Huffmana dla znaku: tworzy go ciąg etykiet krawędzi od korzenia do liścia z danym znakiem.
Dla naszego drzewa :

Znak Kod
Z1 00
Z2 01
Z3 10
Z4 110
Z5 111

Jak widać kody te nie mają równej długości, ze sposobu tworzenia drzewa wynika fakt, że znaki o większej wartości f mają krótsze kody.
Budowa tego drzewa następuje poprzez scalanie poddrzew. Początkowo każdy znak tworzy odrębne poddrzewo, waga korzenia jest równa liczbie f danego znaku.
Algorytm przebiega następująco:

1 Dodaj do posortowanej kolejki Q wszystkie znaki z alfabetu A
2 Wybierz dwa drzewa o najmniejszej wadze w korzeniu
3 Scal te drzewa i zsumuj wagi ich korzeni, przypisz tą sumę korzeniowi nowego drzewa
4 Wstaw nowe drzewo do kolejki (sortując ją)
5 Jeżeli w kolejce jest więcej niż jedno drzewo, wróć do 2.

Po utworzeniu drzewa należy nadać etykiety krawędziom: lewym 0 i prawym 1. Następnie można już odczytywać kody znaków.
Kompresowanie polega na zastąpieniu ciągu bitów pliku wejściowego konkatenacją kodów Huffmana poszczególnych znaków.
Dekompresja to opisany powyżej rozbiór ciągu bitów pliku skompresowanego na kody Huffmana i odczytanie odpowiednich znaków.
Jak widać, jest to metoda trochę trudniejsza niż stosowanie kodów o stałej długości. Zobaczmy, czy ten wysiłek się opłaca. Przeanalizujmy ten sam plik o wielkości 1MB składający się z ciągu znaków z alfabetu A={a, b, c, d, e} o następujących częstościach wystąpień:
f(a)=187.723, f(b)=506.035, f(c)=102.060, f(d)=125.457, f(e)=127.301. Oczywiście f(a)+f(b)+f(c)+f(d)+f(e)=1048576 bajtów, czyli 1MB.
Zgodnie z algorytmem znaki te początkowo tworzą odrębne drzewa o wadze korzenia równej liczbie f, umieszczamy je zatem w kolejce posortowanej niemalejąco wg wag:

Wybieramy dwa pierwsze drzewa (na najmniejszej wadze korzeni) i łączymy je w jedno drzewo sumując wagi korzeni a następnie wstawiamy nowe drzewo do kolejki (na trzecie miejsce, gdyż waga korzenia nowego drzewa wynosi 227.517):

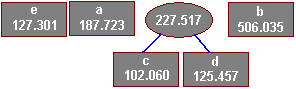
Tworzymy kolejne drzewo, tym razem ze znaków e i a:

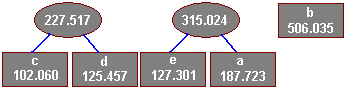
Teraz dwa pierwsze elementy są prawdziwymi drzewami, scalamy ich korzenie w nowe drzewo:

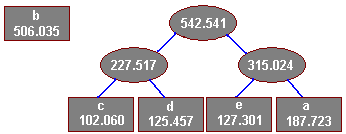
Scalamy ostatnie dwa drzewa w całość i nadajemy krawędziom etykiety:

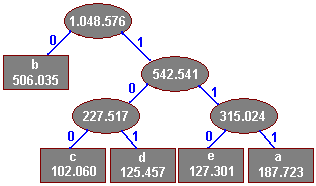
Bezpośrednio z drzewa odczytujemy kody znaków

Znak Kod
a 111
b 0
c 100
d 101
e 110

Jak widać, najkrótszy kod ma litera b, która występuje w pliku największą ilość razy, policzmy teraz, ile zyskaliśmy stosując kody o zmiennej długości, wyznaczymy tzw. koszt drzewa, czyli sumę iloczynów długości kodu i liczby wystąpień w pliku. Koszt drzewa jest liczbą bitów potrzebną do zapisania skompresowanego ciągu znaków:
B(T)=3*187.723+1*506.035+3*102.060+3*125.457+3*127.301=2.133.658 bitów, co stanowi 25,4% pliku wejściowego. Kompresując ten sam plik za pomocą kodów o stałej długości otrzymaliśmy 37,5% pliku pierwotnego.
W rzeczywistości należy doliczyć jeszcze kilka bitów do ciągu wynikowego, gdyż liczba 2.133.658 nie dzieli się przez 8, a na komputerze można zapisać jedynie liczby bitów będących wielokrotnością ósemki. Dodajemy więc 6 bitów nieznaczących i otrzymujemy 2.133.664 bitów, co daje 266.708 bajtów (plik wejściowy miał 1MB).